|
Approximations Of π
Approximation#Mathematics, Approximations for the mathematical constant pi () in the history of mathematics reached an accuracy within 0.04% of the true value before the beginning of the Common Era. In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century. Further progress was not made until the 14th century, when Madhava of Sangamagrama developed approximations correct to eleven and then thirteen digits. Jamshīd al-Kāshī achieved sixteen digits next. Early modern mathematicians reached an accuracy of 35 digits by the beginning of the 17th century (Ludolph van Ceulen), and 126 digits by the 19th century (Jurij Vega). The record of manual approximation of is held by William Shanks, who calculated 527 decimals correctly in 1853. Since the middle of the 20th century, the approximation of has been the task of electronic digital computers (for a comprehensive account, see chronology of computation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
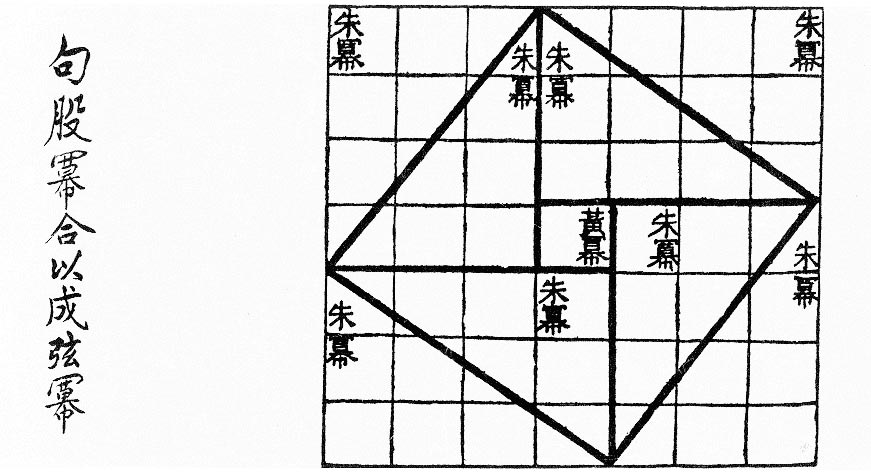
Squaring The Circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square (geometry), square with the area of a circle, area of a given circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of Line (geometry), lines and circles implied the existence of such a square. In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (\pi) is a transcendental number. That is, \pi is not the zero of a function, root of any polynomial with Rational number, rational coefficients. It had been known for decades that the construction would be impossible if \pi were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, an addition of Infinity, infinitely many Addition#Terms, terms, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures in combinatorics through generating functions. The mathematical properties of infinite series make them widely applicable in other quantitative disciplines such as physics, computer science, statistics and finance. Among the Ancient Greece, Ancient Greeks, the idea that a potential infinity, potentially infinite summation could produce a finite result was considered paradoxical, most famously in Zeno's paradoxes. Nonetheless, infinite series were applied practically by Ancient Greek mathematicians including Archimedes, for instance in the Quadrature of the Parabola, quadrature of the parabola. The mathematical side of Zeno's paradoxes was resolved using the concept of a limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chinese Mathematics
Mathematics emerged independently in China by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system (base 2, binary and base 10, decimal), algebra, geometry, number theory and trigonometry. Since the Han dynasty, as diophantine approximation being a prominent numerical method, the Chinese made substantial progress on polynomial evaluation. Algorithms like regula falsi and expressions like simple continued fractions are widely used and have been well-documented ever since. They deliberately find the principal nth root, ''n''th root of positive numbers and the zero of a function, roots of equations. The major texts from the period, ''The Nine Chapters on the Mathematical Art'' and the ''Book on Numbers and Computation'' gave detailed processes for solving various mathematical problems in daily life. All procedures were computed using a counting board in both texts, and they ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenistic Sicily, Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and mathematical analysis, analysis by applying the concept of the Cavalieri's principle, infinitesimals and the method of exhaustion to derive and rigorously prove many geometry, geometrical theorem, theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supercomputer
A supercomputer is a type of computer with a high level of performance as compared to a general-purpose computer. The performance of a supercomputer is commonly measured in floating-point operations per second (FLOPS) instead of million instructions per second (MIPS). Since 2022, supercomputers have existed which can perform over 1018 FLOPS, so called Exascale computing, exascale supercomputers. For comparison, a desktop computer has performance in the range of hundreds of gigaFLOPS (1011) to tens of teraFLOPS (1013). Since November 2017, all of the TOP500, world's fastest 500 supercomputers run on Linux-based operating systems. Additional research is being conducted in the United States, the European Union, Taiwan, Japan, and China to build faster, more powerful and technologically superior exascale supercomputers. Supercomputers play an important role in the field of computational science, and are used for a wide range of computationally intensive tasks in various fields, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine. Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometrical expressions with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation. History Sumerian astronomers studied angle me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Mathematics
Ancient Greek mathematics refers to the history of mathematical ideas and texts in Ancient Greece during Classical antiquity, classical and late antiquity, mostly from the 5th century BC to the 6th century AD. Greek mathematicians lived in cities spread around the shores of the ancient Mediterranean, from Anatolia to Italy and North Africa, but were united by Greek culture and the Ancient Greek, Greek language. The development of mathematics as a theoretical discipline and the use of deductive reasoning in Mathematical proof, proofs is an important difference between Greek mathematics and those of preceding civilizations. The early history of Greek mathematics is obscure, and traditional narratives of Theorem, mathematical theorems found before the fifth century BC are regarded as later inventions. It is now generally accepted that treatises of deductive mathematics written in Greek began circulating around the mid-fifth century BC, but the earliest complete work on the subje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indian Mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta, Bhaskara II, Varāhamihira, and Madhava of Sangamagrama, Madhava. The Decimal, decimal number system in use today: "The measure of the genius of Indian civilisation, to which we owe our modern (number) system, is all the greater in that it was the only one in all history to have achieved this triumph. Some cultures succeeded, earlier than the Indian, in discovering one or at best two of the characteristics of this intellectual feat. But none of them managed to bring together into a complete and coherent system the necessary and sufficient conditions for a number-system with the same potential as our own." was first recorded in Indian mathematics. Indian mathematicians made early contributions to the study of the concept of 0 (number), ze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pi (letter)
Pi (; Ancient Greek or , uppercase Π, lowercase π, cursive ϖ; ) is the sixteenth letter of the Greek alphabet, representing the voiceless bilabial plosive . In the system of Greek numerals it has a value of 80. It was derived from the Phoenician alphabet, Phoenician letter Pe (Semitic letter), Pe (). Letters that arose from pi include Latin alphabet, Latin P, Cyrillic script, Cyrillic Pe (Cyrillic), Pe (П, п), Coptic alphabet, Coptic pi (Ⲡ, ⲡ), and Gothic alphabet, Gothic pairthra (𐍀). Uppercase Pi The uppercase letter Π is used as a symbol for: * In textual criticism, ''Codex Petropolitanus (New Testament), Codex Petropolitanus'', a 9th-century uncial codex of the Gospels, now located in St. Petersburg, Russia. * In legal shorthand, it represents a plaintiff. * In Mathematical finance, it represents a portfolio. Greek letters used in mathematics, science, and engineering, In science and engineering: * The product (mathematics), product operator in mathematics, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |